Сапер и его вариации
За все то время, пока мы игрались с физикой в world of goo и crayon, восторгались шейдерам в gravity bone и перемоткой времени в groundhog старый-добрый сапер обзавелся несколькими производными.
Первая из них — Minesweeper3D — обычный трехмерный сапер без затей. Можно выбирать "объем" поля и его форму (куб/шар). Игра полностью фриварная, здесь находится версия для windows.

Mines3d чуть необычнее, в качестве поля нам предлагают разнообразные геометрические фигуры, среди них куб, октаэдр, звездчатый октаэдр и додекаэдр. Одно но — игра триальная и в бесплатной версии некоторые опции заблокированы. Ссылка на страницу игры

Super Minesweeper, хоть и двумерный, но имеет свою прелесть. Клетки могут быть какими угодно, на выбор пользователя: прямоугольными, однобокими трапециями, гексагонами (иначе — шестиугольниками), а также их смесями. Есть интересные фичи вроде перемещения бомб и разных режимов игры. В одном из них при генерации поля в одной клетке может находиться несколько мин. В другом их можно двигать. В третьем вместо количества рядомстоящих мин номер в клетке показывает расстояние до ближайшей мины. Увы, поделие тоже шароварное, а ознакомиться с демкой можно на странице игры.

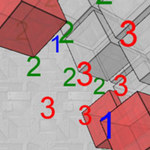
И напоследок самый жир - Minefield6D. Да, это самый что ни на есть шестимерный сапер (вообще количество измерений выбирает пользователь, возможный диапазон — 2-10). Представлен он не проекцией многомерного объекта на двумерную плоскость монитора, а в разрезе, для наглядности и в угоду геймплею (что хорошо и логично). Игра кажется сложной для понимания, но только на первый взгляд, к тому же с ней идет небольшой учебник, в котором все доходчиво изложено.
Можно скачать игру (к слову, полностью бесплатную) или посетить страничку автора (кстати, нашего соотечественника).

Предлагаю делиться в комментариях всем, что связано с многомерностью или нестандартными формами: многомерными змейками, пакманами, четырехмерными тетрисами, несимметричными кубиками рубика, одномерными саперами (для блондинок), нуль-мерными (для дзен-буддистов), аркадами с неевклидовой геометрией, трехмерными шахматами или бильярдом, интересны любые извращения.
- 09 июня 2009, 18:54
- 01



8 комментариев